La magia de los círculos
Fase comarcal de Alicante de la XX Olimpiada Matemática, 2009
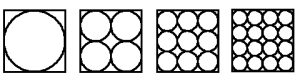
En la imagen aparece un cuadrado de lado una unidad en el que se inscribe primero un círculo, después cuatro, después nueve, y, finalmente, 16.
Calcula la relación en cada caso entre el área del cuadrado y la suma del área del total de círculos inscritos.
¿Cuál sería la relación si inscribiésemos 10x10 = 100 círculos en el cuadrado? ¿Por qué?



6 comentarios:
Com és evident, el nombre de cercles per quadrat és una successió de terme general n^2. Així, podrem elaborar una àrea general i no caldrà que provem per a cada cas.
Com que els cercles són tangents, la suma dels diàmetres dels cercles d'una filera o columna és igual al costat del quadrat. En cada fila hi ha n quadrats, per tant el ràdi de cada cercle és: c/2n on c és el costat del quadrat.
L'àrea d'un cercle és, per tant: pi*c^2/4n^2, i l'àrea total, seria aquesta pel nombre de cercles n^2, Amb el que queda que l'àrea no depén de n.
La relació 4*c^2/pi*c^2 = 4/pi, que és la relació entre l'àrea del quadrat i la de la suma dels cercles, es manté constant independentment del nombre de cercles inscrits.
Hola
Para la primera imagen, sería:
(2r)²/pi•r²
Para la segunda imagen sería:
(4r)²/4(pi•r²)
Y así con todas
Para 100 círculos sería:
(20r)²/100(pi•r²)
Para x círculos:
((raiz ² de x)•2)²/x(pi•r²)
Hasta otra...
salu2
Ignacio
logicayestrategia.blogspot.com
Siendo n el numero de circulos inscritos seria:
Pi / n
Hice el calculo y si decimos que el lado del cuadrado = 1 tanto el area del cuadrado como el area de los circulos permanece constante
POr obviedad el area del cuadrado siempre es 1..
Primera imagen
r= 1/2 = 0.5
0.5^2 por Pi = 0.785398163
Segunda
r= 1/4 = 0.25
4(0.25^2 por Pi) = 0.7853963
Tercera
r = 1/6= .1666
9(0.1666^2 por Pi) = 0.7853963
Y asi para todas numero cuadrado de circulos interiores
Por tanto la relacion es 1/0.7853963
para mi todos los circulos funcionan como una unidad, cada area del circulo equivale a 1 y por lo tanto 10x10=100
Dado que en el primer caso tenemos cuadrado lado=diamentro=2 radios menos circulo = r^2 (4-pi) es la diferencia en los siguientes casos el radio se divide entre el numero de circulos de lado y se multiplica por la cantidad de circulos
((r/n)²(4-pi))n²=n²(r²/n²)(4-pi)=r²(4-pi)
por lo tanto la diferencia es constante por tanto sustituyo l=1 d=1 r=1/2
(1/4)(4-pi)=1-pi/4
Publicar un comentario