Este blog estaba escrito para plantear problemas de matemáticas, con objeto de entrenar a mis alumnos para presentarse a concursos de resolución de problemas (como la Olimpiada Matemática). Tiene un blog hermano donde publicaba las soluciones. De momento, está pendiente de recuperar algo de tiempo y ganas para continuar. La frecuencia de publicación será semanal, y las soluciones se publicarán con cierto retraso respecto al enunciado.
Dividir en cuatro zonas
Fase autonómica de la XXI Olimpiada Matemática de la Comunidad Valenciana, 2010
En una trama de 9 puntos se ha dibujado un cuadrado.
Encuentra todas las formas distintas de conseguir 4 zonas de igual área uniendo puntos de la trama mediante líneas rectas, como se muestra en el ejemplo.
Si quieres colaborar con el blog, o contactar con el autor, deja un comentario en cualquiera de las entradas.
Leo todos los comentarios antes de que se publiquen, así que si dejas información sensible (correo electrónico, por ejemplo) lo borraré antes de que lo vea alguien más.
Esta obra está bajo una licencia de Creative Commons.
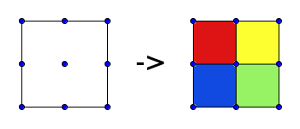
5 comentarios:
Es obvio que para hacerlo hay que unir los puntos diagonalmente:
Hay 8 formas de hacerlo mediante 4 triángulos rectangulos (desde un punto del centro de la línea a una esquina) otra haciendo 4 triángulos isósceles y la de los cuadrados.
10 en total creo yo
Yo encuentro 6 maneras, para mayor claridad uso números para nombrar los nodos:
123
456
789
La primera trazando dos lineas 2,8 y 4,6 obtenemos 4 cuadrados, solución única.
La segunda trazando las diagonales 1,9 y 3,7 obtenemos cuatro triángulos recángulos, también única.
La última sería trazando la recta 4,6 y dos diagonales 1,6 y 4,9. Esta distribución se puede rotar y reflejar por lo que obtenemos 4 opciones más en total.
yo he encontrado 13 contando la primera, osea 12 mas.
18, 28, 29, y todas sus reflecciones (4)
18, 28, 83, y todas sus reflecciones (4)
18, 19, 16, y todas sus reflecciones (4)
en total son 12, mas la primera son 13 formas distintas
se me olvido colocar las diagonales xD,
19, 37, jajajajaja
yo tengo 5 formas que las de la solucion
Publicar un comentario