Triángulos mágicos
(Fase comarcal de la XVIII Olimpiada Matemática, 2007)
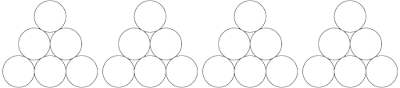
Utiliza las figuras siguientes para colocar dentro de cada círculo un número de 1 a 6, sin repetir ninguno dentro de un mismo triángulo de círculos, y de forma que cada arista sume 12 en el primer triángulo, 9 en el segundo, 10 en el tercero y 11 en el cuarto. ¿Podrías lograr con estos mismos números que un triángulo de ese tipo sumase 13 o que sumase 8? Razona tu respuesta.



3 comentarios:
la respuesta esta ordenada por fila de arriba hacia abajo por figura
firura 1:
5-1,3-6,2,4
figura 2:
2-6,4-1,5,3
figura 3:
3-2,6-5,4,1
figura 4:
4-5,1-2,3,6
eso seria lo de las figuras, pero la respuesta a lo otro segun io es no...
pero aun estoi evaluando las razones
dentro de la semana las subo
Es imposible que sumen 13 y 8 porque no se pueden combinar los numeros sin que se repitan, solo son posibles estas dos soluciones para cada numero.
.13=6+5+2
13=6+4+3
.8=5+2+1
8=4+3+1
Supongamos que x,y,z son los vértices del triángulo (por ejemplo, x el superior, y el izquierdo y z el derecho) y que a esté entre x e y, b entre x z, c entre y z. De esta manera tengo la fila inferior del triángulo que es ycz, la segunda fila será ab y arriba x. Supongamos que quiero que los lados sumen k. De esta manera tengo:
x+a+y=k, x+b+z=k, y+c+z=k.
Si sumo las tres ecuaciones tengo
x+y+z+(x+y+z+a+b+c)=3k
El paréntesis suma 21 ya que x,y,z,a,b,c son los números del 1 al 6 (1+2+3+4+5+6=21), por tanto:
x+y+z=3k-21
De las condiciones del problema sabemos que x+y+z>=1+2+3=6 y que x+y+z<=4+5+6=15. Por tanto,
6<=3k-21<=15
O sea, 27<=3k<=36
Es decir 9<=k<=12
Ello indica que los valores posibles para una suma de los elementos de los lados están entre 9 y 12, ambos inclusive; lo cual significa que NO es posible que la suma sea 8 o 13.
Publicar un comentario